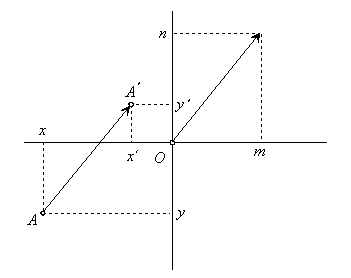Транслация
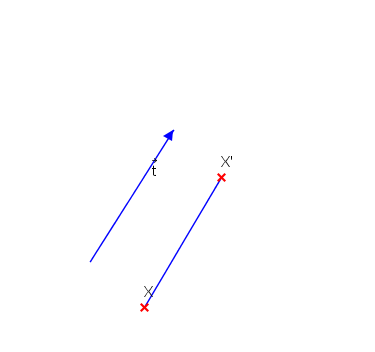
Определение:Преобразувание в равнината, при което на произволна точка Х се съпоставя точката Х’,за която ХХ’→ = t→, къдетоt→ е даден вектор, се нарича транслация или успоредно пренасяне.
Теорема: Всякатранслация е еднаквост.
права е успоредна на нея праваили същата права
Следствие: При транслациятаобразът на:
отсечка е успоредна и равна нанея отсечка;права е успоредна на нея праваили същата права
Тъй като транслацията е еднаквост, тя притежававсички свойства на еднаквостите.
Образът на права, която е успореднана векторът на транслацията, е същата права.Образът на триъгълник намираме,като построим образите на върховете му.Образът на окръжност намираме,като постоим образа на ценътъра й.
Транслацията няма двойни точки.Двойни прави на транслацията савсучки прави, които са успоредни на вектора на транслацията.
Приложение на Транслация в живота:
При този тип симетрия обектите остават неизменни при дискретни или непрекъснати транслации.
Елементите от системата се повтарят по строго определени отмествания. Безкрайна равнина се покрива фигури с транслационна симетрия от начална позиция по формулата:
, където kx, ky е кое да е цяло число
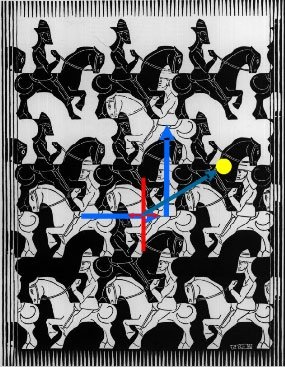
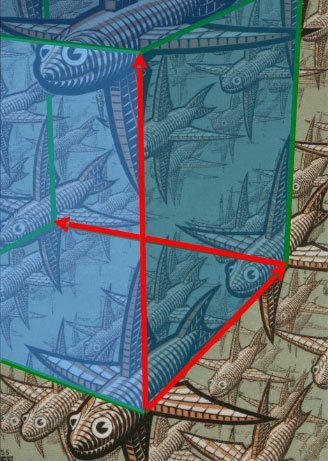
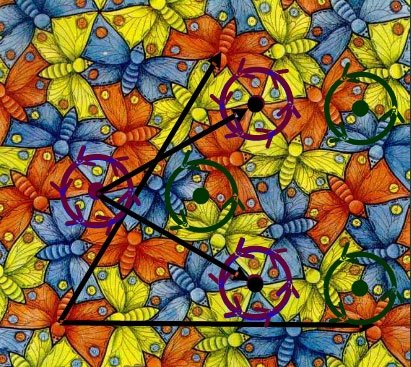
Транслационната симетрия е в основата на мозайките, за които ще има отделна тема. Ако се вгледаме в прочутите мозайки на Ешер ще забележим и транслационната симетрия (тя е в самото определение на патерна, мозайката) и комбинации от всички други симетрии.
Задачи за Транслация:
1зад:В трапец ABCD диагоналите са перпендикулярни и имат дължини 6 и 7. Намерете лицето на трапеца.
2зад:Даден е ΔАВС със страни ВС = а, СА=b,АВ=c и точката М върху лъча АВ така, че АМ = d. а)Постройте образа В1С1 на страната ВС при транслация Т, определена с вектора АМ. Докажете ,че AB1C1C е трапец. в)Намерете страните на трапеца AB1C1C.
3зад:Даден е успоредник АВСD.Намерете при транслация АВ образите на : а)точките D,A и В б) отсечките AD,BD в)триъгълник АВС. ЗАДАЧА.2 Даден е триъгълник АВС.Намерете С'=транслация АВ(С) .Какъв е четириъгълникът АВС'С?
4зад:Даден е триъгълник АВС. При транслация с вектор АВ, С се изобразява в С'. Какъв е четириъгълника АВС'С?